AES 的全称是 Advanced Encryption Standard,意思是高级加密标准。它的出现主要是为了取代 DES 加密算法的,反正就是随着计算机算力的提升,DES 越来越没有那么安全了,可以被破解,且破解时间不长。上篇写的 DES 加密算法,已经很复杂了,这个 AES 加密算法是取代 DES 加密算法的,可想而知,就更复杂了。
这篇博客本来只是挂了一下 AES 加密算法的特征值识别和特征运算,奈何最近做题,发现自己对 AES 加密算法根本不熟悉,有时候仅仅通过 S 盒来识别并不保险,在 IDA 中一堆的混淆代码也很难看出特征运算特征 AES 是一个非常重要的加密算法。故重新学习,并且要做到能看代码识别出加密流程。
密码学基础:AES 加密算法 – 知乎 (zhihu.com)
AES 加密算法原理的详细介绍与实现 - CSDN 博客
后面的内容大部分可能只是对别人博客的复制粘贴,因为写的太好了,留着自己看。
AES 为分组密码,分组密码也就是把明文分成一组一组的,每组长度相等,每次加密一组数据,直到加密完整个明文。SM4、BlowFish 这种似乎都是分组密码,我对这类型的加密算法也是最不熟悉的,因为真的很复杂,处理很多。
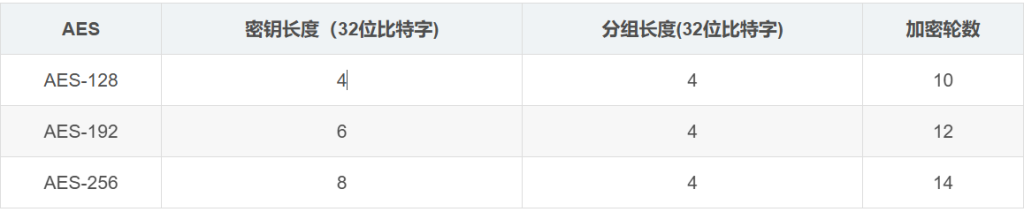
在 AES 标准规范中,分组长度只能是 128 位,也就是说,每个分组为 16 个字节(每个字节 8 位)。密钥的长度可以使用 128 位、192 位或 256 位。密钥的长度不同,推荐加密轮数也不同,如下图所示:
做题遇到比较多的好像还是 AES-128。
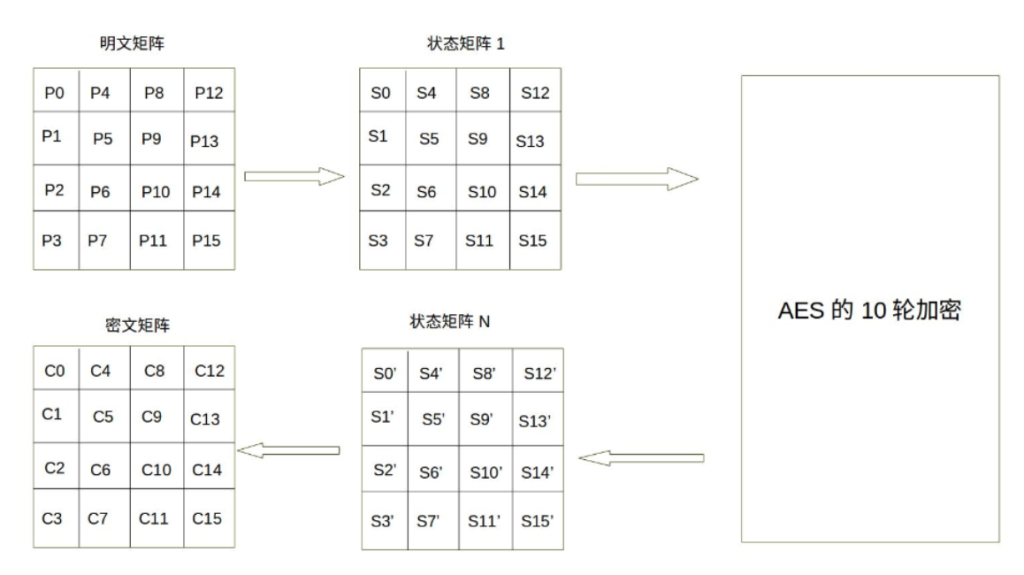
AES 的处理单位是字节,128 位的输入明文分组 P 和输入密钥 K 都被分成 16 个字节,分别记为 P = P0 P1 … P15 和 K = K0 K1 … K15 。如,明文分组为 P = abcdefghijklmnop, 其中的字符 a 对应 P0 ,p 对应 P15 。一般地,明文分组用字节为单位的正方形矩阵描述,称为状态矩阵。在算法的每一轮中,状态矩阵的内容不断发生变化,最后的结果作为密文输出。该矩阵中字节的排列顺序为从上到下、从左至右依次排列,如下图所示。
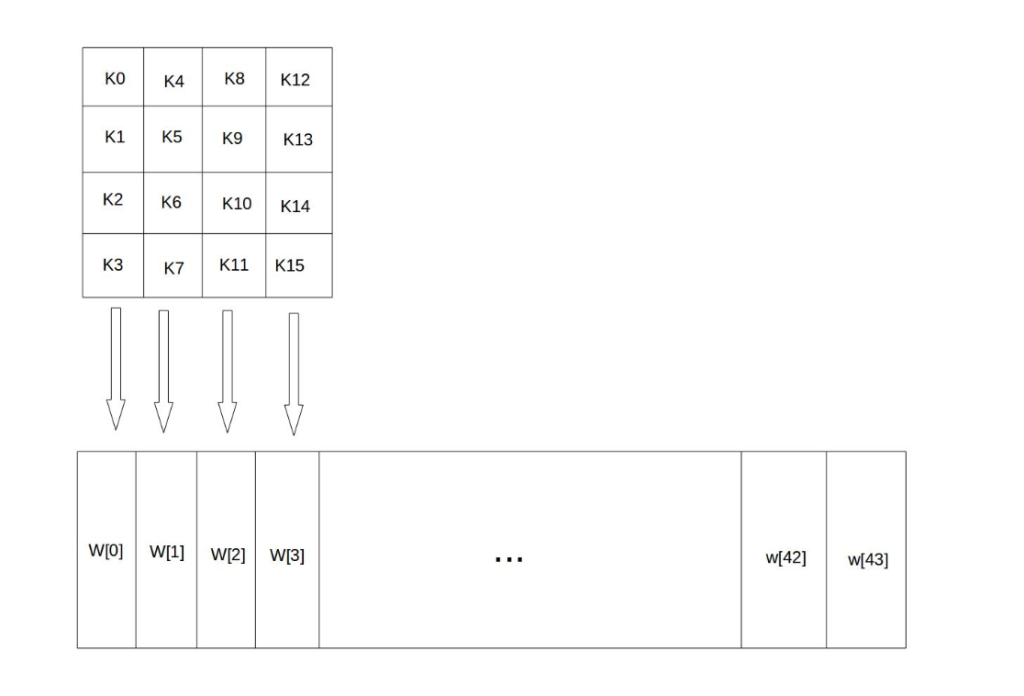
128 位密钥也是用字节为单位的矩阵表示,矩阵的每一列被称为 1 个 32 位比特字。通过密钥编排函数该密钥矩阵被扩展成一个 44 个字组成的序列 W [0],W [1], … ,W [43], 该序列的前 4 个元素 W [0],W [1],W [2],W [3] 是原始密钥,用于加密运算中的初始密钥加(下面介绍); 后面 40 个字分为 10 组,每组 4 个字(128 比特)分别用于 10 轮加密运算中的轮密钥加,如下图所示:
上图中,设 K = “abcdefghijklmnop”,则 K0 = a, K15 = p, W[0] = K0 K1 K2 K3 = “abcd”。
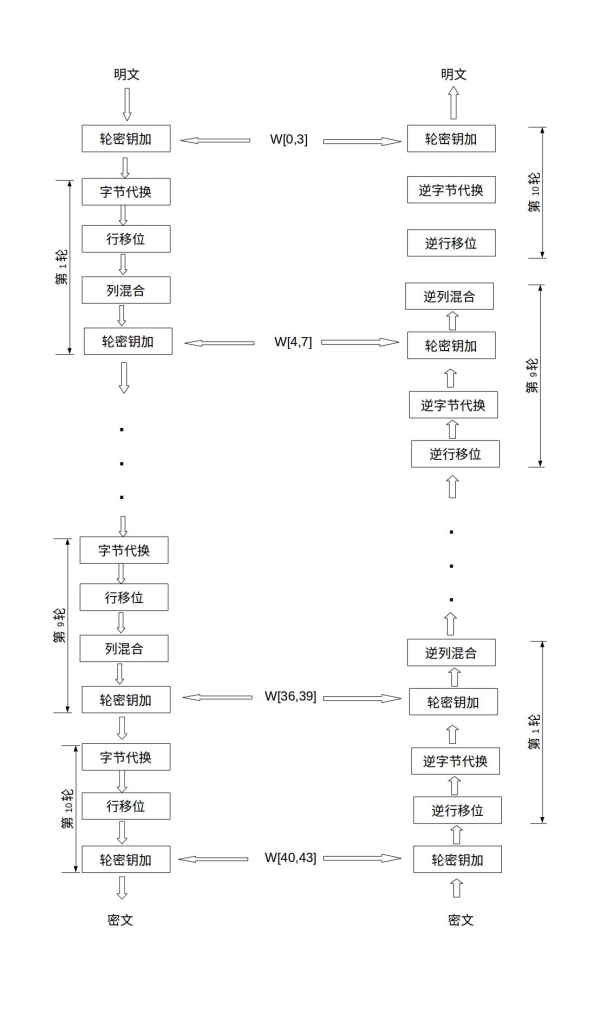
AES 的整体结构如下图所示,其中的 W [0,3] 是指 W [0]、W [1]、W [2] 和 W [3] 串联组成的 128 位密钥。加密的第 1 轮到第 9 轮的轮函数一样,包括 4 个操作:字节代换、行位移、列混合和轮密钥加。最后一轮迭代不执行列混合。另外,在第一轮迭代之前,先将明文和原始密钥进行一次异或加密操作。
上图也展示了 AES 解密过程,解密过程仍为 10 轮,每一轮的操作是加密操作的逆操作。由于 AES 的 4 个轮操作都是可逆的,因此,解密操作的一轮就是顺序执行逆行移位、逆字节代换、轮密钥加和逆列混合。同加密操作类似,最后一轮不执行逆列混合,在第 1 轮解密之前,要执行 1 次密钥加操作。
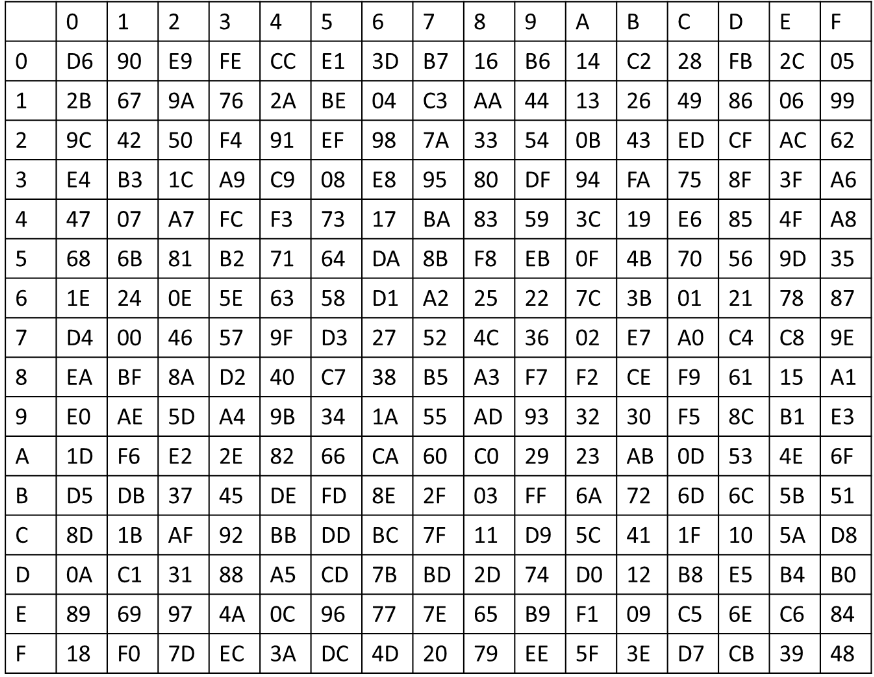
AES 的字节代换其实就是一个简单的查表操作。AES 定义了一个 S 盒和一个逆 S 盒。
static const int S[16 ][16 ] = { 0x63 , 0x7c , 0x77 , 0x7b , 0xf2 , 0x6b , 0x6f , 0xc5 , 0x30 , 0x01 , 0x67 , 0x2b , 0xfe , 0xd7 , 0xab , 0x76 ,
0xca , 0x82 , 0xc9 , 0x7d , 0xfa , 0x59 , 0x47 , 0xf0 , 0xad , 0xd4 , 0xa2 , 0xaf , 0x9c , 0xa4 , 0x72 , 0xc0 ,
0xb7 , 0xfd , 0x93 , 0x26 , 0x36 , 0x3f , 0xf7 , 0xcc , 0x34 , 0xa5 , 0xe5 , 0xf1 , 0x71 , 0xd8 , 0x31 , 0x15 ,
0x04 , 0xc7 , 0x23 , 0xc3 , 0x18 , 0x96 , 0x05 , 0x9a , 0x07 , 0x12 , 0x80 , 0xe2 , 0xeb , 0x27 , 0xb2 , 0x75 ,
0x09 , 0x83 , 0x2c , 0x1a , 0x1b , 0x6e , 0x5a , 0xa0 , 0x52 , 0x3b , 0xd6 , 0xb3 , 0x29 , 0xe3 , 0x2f , 0x84 ,
0x53 , 0xd1 , 0x00 , 0xed , 0x20 , 0xfc , 0xb1 , 0x5b , 0x6a , 0xcb , 0xbe , 0x39 , 0x4a , 0x4c , 0x58 , 0xcf ,
0xd0 , 0xef , 0xaa , 0xfb , 0x43 , 0x4d , 0x33 , 0x85 , 0x45 , 0xf9 , 0x02 , 0x7f , 0x50 , 0x3c , 0x9f , 0xa8 ,
0x51 , 0xa3 , 0x40 , 0x8f , 0x92 , 0x9d , 0x38 , 0xf5 , 0xbc , 0xb6 , 0xda , 0x21 , 0x10 , 0xff , 0xf3 , 0xd2 ,
0xcd , 0x0c , 0x13 , 0xec , 0x5f , 0x97 , 0x44 , 0x17 , 0xc4 , 0xa7 , 0x7e , 0x3d , 0x64 , 0x5d , 0x19 , 0x73 ,
0x60 , 0x81 , 0x4f , 0xdc , 0x22 , 0x2a , 0x90 , 0x88 , 0x46 , 0xee , 0xb8 , 0x14 , 0xde , 0x5e , 0x0b , 0xdb ,
0xe0 , 0x32 , 0x3a , 0x0a , 0x49 , 0x06 , 0x24 , 0x5c , 0xc2 , 0xd3 , 0xac , 0x62 , 0x91 , 0x95 , 0xe4 , 0x79 ,
0xe7 , 0xc8 , 0x37 , 0x6d , 0x8d , 0xd5 , 0x4e , 0xa9 , 0x6c , 0x56 , 0xf4 , 0xea , 0x65 , 0x7a , 0xae , 0x08 ,
0xba , 0x78 , 0x25 , 0x2e , 0x1c , 0xa6 , 0xb4 , 0xc6 , 0xe8 , 0xdd , 0x74 , 0x1f , 0x4b , 0xbd , 0x8b , 0x8a ,
0x70 , 0x3e , 0xb5 , 0x66 , 0x48 , 0x03 , 0xf6 , 0x0e , 0x61 , 0x35 , 0x57 , 0xb9 , 0x86 , 0xc1 , 0x1d , 0x9e ,
0xe1 , 0xf8 , 0x98 , 0x11 , 0x69 , 0xd9 , 0x8e , 0x94 , 0x9b , 0x1e , 0x87 , 0xe9 , 0xce , 0x55 , 0x28 , 0xdf ,
0x8c , 0xa1 , 0x89 , 0x0d , 0xbf , 0xe6 , 0x42 , 0x68 , 0x41 , 0x99 , 0x2d , 0x0f , 0xb0 , 0x54 , 0xbb , 0x16 };
static const int S2[16 ][16 ] = { 0x52 , 0x09 , 0x6a , 0xd5 , 0x30 , 0x36 , 0xa5 , 0x38 , 0xbf , 0x40 , 0xa3 , 0x9e , 0x81 , 0xf3 , 0xd7 , 0xfb ,
0x7c , 0xe3 , 0x39 , 0x82 , 0x9b , 0x2f , 0xff , 0x87 , 0x34 , 0x8e , 0x43 , 0x44 , 0xc4 , 0xde , 0xe9 , 0xcb ,
0x54 , 0x7b , 0x94 , 0x32 , 0xa6 , 0xc2 , 0x23 , 0x3d , 0xee , 0x4c , 0x95 , 0x0b , 0x42 , 0xfa , 0xc3 , 0x4e ,
0x08 , 0x2e , 0xa1 , 0x66 , 0x28 , 0xd9 , 0x24 , 0xb2 , 0x76 , 0x5b , 0xa2 , 0x49 , 0x6d , 0x8b , 0xd1 , 0x25 ,
0x72 , 0xf8 , 0xf6 , 0x64 , 0x86 , 0x68 , 0x98 , 0x16 , 0xd4 , 0xa4 , 0x5c , 0xcc , 0x5d , 0x65 , 0xb6 , 0x92 ,
0x6c , 0x70 , 0x48 , 0x50 , 0xfd , 0xed , 0xb9 , 0xda , 0x5e , 0x15 , 0x46 , 0x57 , 0xa7 , 0x8d , 0x9d , 0x84 ,
0x90 , 0xd8 , 0xab , 0x00 , 0x8c , 0xbc , 0xd3 , 0x0a , 0xf7 , 0xe4 , 0x58 , 0x05 , 0xb8 , 0xb3 , 0x45 , 0x06 ,
0xd0 , 0x2c , 0x1e , 0x8f , 0xca , 0x3f , 0x0f , 0x02 , 0xc1 , 0xaf , 0xbd , 0x03 , 0x01 , 0x13 , 0x8a , 0x6b ,
0x3a , 0x91 , 0x11 , 0x41 , 0x4f , 0x67 , 0xdc , 0xea , 0x97 , 0xf2 , 0xcf , 0xce , 0xf0 , 0xb4 , 0xe6 , 0x73 ,
0x96 , 0xac , 0x74 , 0x22 , 0xe7 , 0xad , 0x35 , 0x85 , 0xe2 , 0xf9 , 0x37 , 0xe8 , 0x1c , 0x75 , 0xdf , 0x6e ,
0x47 , 0xf1 , 0x1a , 0x71 , 0x1d , 0x29 , 0xc5 , 0x89 , 0x6f , 0xb7 , 0x62 , 0x0e , 0xaa , 0x18 , 0xbe , 0x1b ,
0xfc , 0x56 , 0x3e , 0x4b , 0xc6 , 0xd2 , 0x79 , 0x20 , 0x9a , 0xdb , 0xc0 , 0xfe , 0x78 , 0xcd , 0x5a , 0xf4 ,
0x1f , 0xdd , 0xa8 , 0x33 , 0x88 , 0x07 , 0xc7 , 0x31 , 0xb1 , 0x12 , 0x10 , 0x59 , 0x27 , 0x80 , 0xec , 0x5f ,
0x60 , 0x51 , 0x7f , 0xa9 , 0x19 , 0xb5 , 0x4a , 0x0d , 0x2d , 0xe5 , 0x7a , 0x9f , 0x93 , 0xc9 , 0x9c , 0xef ,
0xa0 , 0xe0 , 0x3b , 0x4d , 0xae , 0x2a , 0xf5 , 0xb0 , 0xc8 , 0xeb , 0xbb , 0x3c , 0x83 , 0x53 , 0x99 , 0x61 ,
0x17 , 0x2b , 0x04 , 0x7e , 0xba , 0x77 , 0xd6 , 0x26 , 0xe1 , 0x69 , 0x14 , 0x63 , 0x55 , 0x21 , 0x0c , 0x7d };
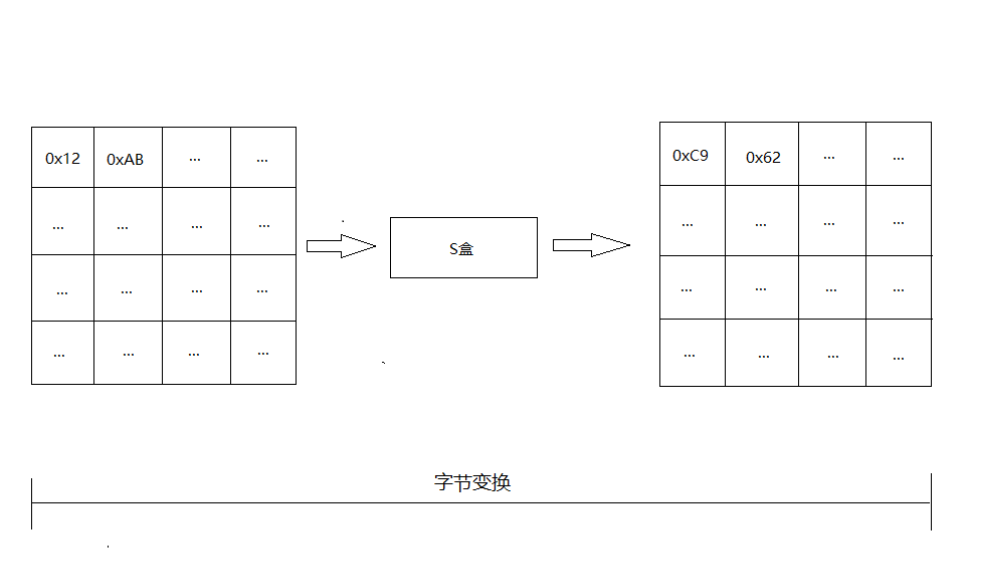
状态矩阵中的元素按照下面的方式映射为一个新的字节:把该字节的高 4 位作为行值,低 4 位作为列值,取出 S 盒或者逆 S 盒中对应的行的元素作为输出。例如,加密时,输出的字节 S1 为 0x12, 则查 S 盒的第 0x01 行和 0x02 列,得到值 0xc9, 然后替换 S1 原有的 0x12 为 0xc9,状态矩阵经字节代换后的图如下:
这里的查表操作和 SM4 加密算法的查表操作是一样的,就是把 S 盒的输入转化为十六进制的形式,然后高位为行,低位为列。
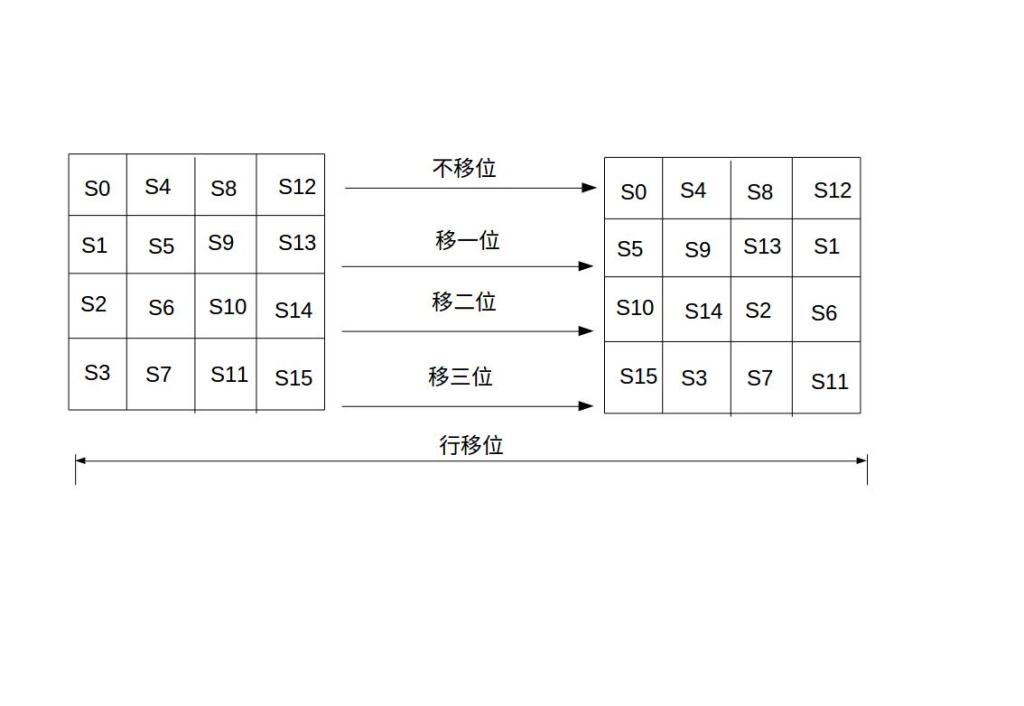
行移位是一个简单的左循环移位操作。当密钥长度为 128 比特时,状态矩阵的第 0 行左移 0 字节,第 1 行左移 1 字节,第 2 行左移 2 字节,第 3 行左移 3 字节,如下图所示:
行移位的逆变换是将状态矩阵中的每一行执行相反的移位操作,例如 AES-128 中,状态矩阵的第 0 行右移 0 字节,第 1 行右移 1 字节,第 2 行右移 2 字节,第 3 行右移 3 字节。