学习大名鼎鼎的RSA加密算法，这玩意在密码学Crypto里面经常会遇到，杂项也有。逆向里面似乎也有，虽然我没遇见过，翻看《加密与解密》里面倒是有RSA的应用。所以还是学习一下，谁还没有一个全栈的梦想呢，

RSA是第一个既能用于数据加密也能用于数字签名的算法，易于理解和操作，应用广泛。该算法以发明家的名字命名——Ron Rivest、Adi Shamir、Leonard Adleman。密码分析者既不能证明也不能否定RSA的发明性，但这恰恰说明该算法有一定的可信度。（这里和下面笔记有部分来自《加密与解密》）

这个加密算法是比较重要的，所以我觉得是应该认真学习一下的。在了解这个加密算法之前，学一下有关的数论知识，有关博客

RSA算法原理（一） – 阮一峰的网络日志 (ruanyifeng.com)

数论知识

1.互质关系

如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。

这个比较好理解，相关结论也一样好理解。

2.欧拉函数

欧拉函数，以φ(n)表示，表示的是小于等于n和n互质的数的个数。

第一种情况：如果n=1，则 φ(1) = 1 。因为1与任何数（包括自身）都构成互质关系。

第二种情况：如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。

第三种情况：如果n是质数的某一个次方，即 n = p^k(p为质数，k为大于等于1的整数)，则φ(p^k)=p^k−p^k−1

显然，一个数不是质数p的倍数时，才可能与n互质，而是质数p的倍数的数一共有p^k−1个，即1×p、2×p、3×p、…、p^k-1×p，这很好理解，把它们去除，剩下的就是与n互质的数。

第四种情况：如果n可以分解成两个互质的整数之积

n = p × q

则有

φ(n) = φ(p×q) = φ(p)×φ(q)

即积的欧拉函数等于各个因子的欧拉函数之积。比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。

上面的博客说，这一条定理的证明需要用到中国剩余定理，这里不想再去了解可以简单学习一下思路。

如果a与p1互质(a<p1)，b与p2互质(b<p2)，c与p1p2互质(c<p1p2)，则c与数对 (a,b) 是一一对应关系。由于a的值有φ(p1)种可能，b的值有φ(p2)种可能，则数对 (a,b) 有φ(p1)φ(p2)种可能，而c的值有φ(p1p2)种可能，所以φ(p1p2)就等于φ(p1)φ(p2)。

这个证明总感觉有点奇怪，这里c和数对一一对应像是利用了排列组合的道理，当然我不懂，乱说而已。

第五种情况：任意一个大于1的正整数，都可以写成一系列质数的积。

n=p₁^k1p₂^k2…p_n^kn

根据第4条的结论，得到

φ(n)=φ(p1p2)=φ(p₁^k1)φ(p₂^k2)…φ(p_n^kn)

再根据第三条结论，得到

φ(n)=p₁^k1p₂^k2…p_n^kn(1-1/p₁)(1-1/p₂)…(1-1/p_n)

即

φ(n)=n(1-1/p₁)(1-1/p₂)…(1-1/p_n)

这就是欧拉函数的通用计算公式。

例如1323的欧拉函数，计算过程如下：
φ(1323)=φ(3³×7²)=1323(1−1/3)(1−1/7)=756

3.同余

给定一个正整数 m，如果两个整数 a 和 b 满足 m|(a-b)，即 a-b 能够被 m 整除，或者 (a-b)/m 得到一个整数，那么就称整数 a 与 b 对模 m 同余，记作 a ≡ b(mod m)。其中符号 ≡ 表示同余，对模 m 同余是整数的一个等价关系。例如：26 ≡ 2(mod 12)。

4.欧拉定理

欧拉定理指的是

若 gcd(a,m) = 1，则a^φ(m) ≡ 1 (mod m)

gcd即求最大公约数（最大公因数）的函数。

不看证明了，记得定理就好，可以看看以下链接，有证明过程

欧拉定理 & 费马小定理 – OI Wiki (oi-wiki.org)

若上面公式中的m为素数，则有a^m-1 ≡ 1 (mod m)，这就是费马小定理。

这也不难理解对吧，如m为素数，可以根据欧拉函数的第二种情况得出。费马小定理是欧拉定理的特例。

5.模反元素

如果两个正整数a和m互质，那么一定可以找到整数b，使得 ab-1 被m整除，或者说ab被m除的余数是1。

ab ≡ 1 (mod m)

 这时，b就叫做a的”模反元素”。

比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}。

即如果b是a的模反元素，则 b+km 都是a的模反元素。

欧拉定理可以用来证明模反元素必然存在。

a^φ(m) = a^{φ(m) -1}×a ≡ 1 (mod m)

可以看到，a的 φ(n)-1 次方相当于b，也就是a的模反元素。

加密

第一步

选取两个大素数(质数)p和q(典型值为1024位，实际应用中，这两个质数越大，就越难破解。)

《加密与解密》说为了获得最高的安全性，两数的长度最好一样，这里涉及数论知识，但是我查不到，等我哪天碰到了就回来补充。

第二步

计算n=pq，n称为模

第三步

计算n的欧拉函数，由第三种情况φ(n) = (p-1)(q-1)

第四步

随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。
实际应用中，e常常选择65537

第五步

计算e对于φ(n)的模反元素d。
即ed ≡ 1 (mod φ(n))
等价于
ed - 1 = kφ(n)

那么我就就可以得到以下的变量

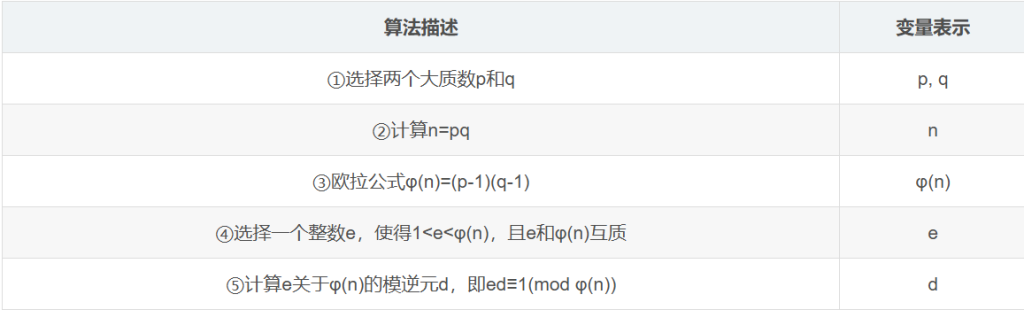
其中公钥就是 Pubkey=(e,n)，私钥Prikey=(d,n)。

给定明文m，加密过程如下：

c ≡ m^e (mod n)，得到的c就是密文。

我们在这里举个例子回顾一下加密的流程，给定质数7、11，对99进行加密

p=7 q=11
n=pq=77
φ(n)=(p-1)(q-1)=60
e=7
#为了方便计算
7d=1(mod 60)->d=43
Pubkey=(7,77)
Prikey=(43,77)
c=997(mod 77)=22

解密

而解密则要用到

c^d ≡ m (mod n)

要证明该解密公式成立，其实就是证明解密得到的结果与明文相同，即

m ≡ c^d(mod n) ≡ m^ed(mod n)

所以只需证明下面公式成立即可

m^ed ≡ m (mod n)

根据加密规则

m^e ≡ c (mod n)

对于同余有

若a ≡ b (mod c)，则a^d ≡ b^d (mod c)

于是有

m^ed ≡ c^d (mod n)

已知

ed ≡ 1 (mod φ(n))，即ed =1 + kφ(n) （k取1、2、3、…、n）

则m^ed = m^1+kφ(n) = m·m^kφ(n) = m·(m^φ(n))^k

若m和n互素，则由欧拉定理得

m^ed ≡ m·(m^φ(n))^k ≡ m·(1)^k ≡ m (mod n)

若m和n不互素，此时，由于n等于质数p和q的乘积，所以m必然等于kp或kq。

以 m = kp为例，考虑到这时k与q必然互质，则根据欧拉定理，下面的式子成立：

(kp)^q-1 ≡ 1 (mod q)

根据同余的性质有

(kp)^k(q-1)(p-1)≡ 1^k(p-1) (mod q) ≡ 1 (mod q)

(kp)^k(q-1)(p-1)×kp ≡ kp (mod q)

又因为ed ≡ 1 (mod φ(n))，ed = kφ(n) + 1

且φ(n) = (p-1)(q-1)，则有

(kp)^ed ≡ kp (mod q) ⇒

(kp)^ed ≡ tq + kp ⇒

(kp)((kp)^ed-1 – 1) ≡ tq

所以tq是可以整除kp的，又因为q是质数，所以显然t能整除p

则t=t₀p

(kp)^ed = t₀pq + kp

又因为m=kp，n=pq，则有

m^ed ≡ m (mod n)

得证。

这证明过程还是很有意思的，值得回味。