本文最后更新于423 天前,其中的信息可能已经过时,如有错误可以直接在文章下留言
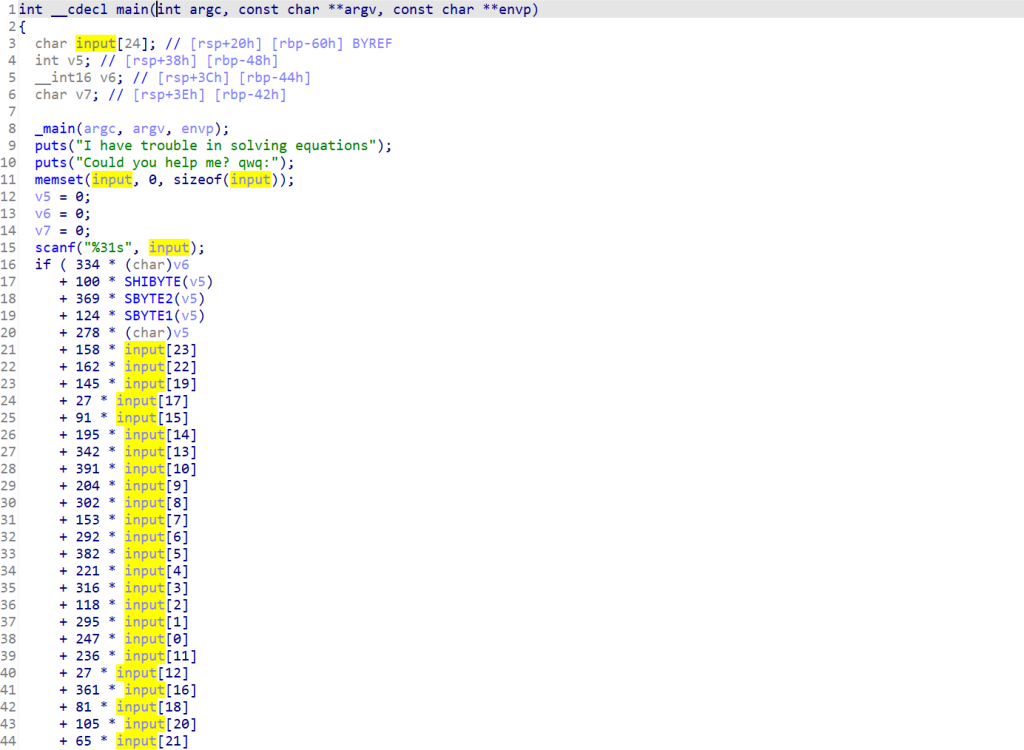
羊城杯有一道题目本来逻辑已经很清晰了,但是因为看不懂算法,还是做不出来,没想到叫DCT,什么狗屎玩意,根本没听过。气死了,只能学习一下,翻DASCTF的一道安卓逆向发现也涉及到DCT,那说明这可能偶尔会出现在题目当中,那就学!
DCT全称为Discrete Cosine Transform,即离散余弦变换。DCT变换属于傅里叶变换的一种,常用于对信号和图像(包括图片和视频)进行数据压缩的基础。
感觉它可能属于某种专业学习的内容,我们这里只学习一下它的公式和算法实现,不去深究它的应用。而且只是学习简单的一维离散余弦变换,因为这玩意有二维的。
参考文章
数字信号处理 — 一维离散余弦变换(python实战)-CSDN博客
离散余弦变换
一维DCT的变换公式如下
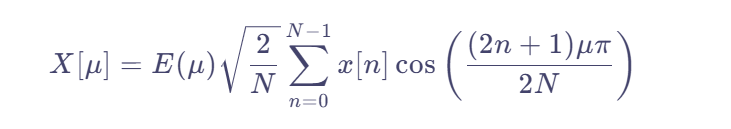
x[n]为输入的离散序列,n的值为0到N-1,N是我们输入的个数
X[μ]为离散余弦变换后的结果,是离散余弦变换的系数,μ的值也为0到N-1
我们假设N为4,则可以将计算等式用矩阵表示。
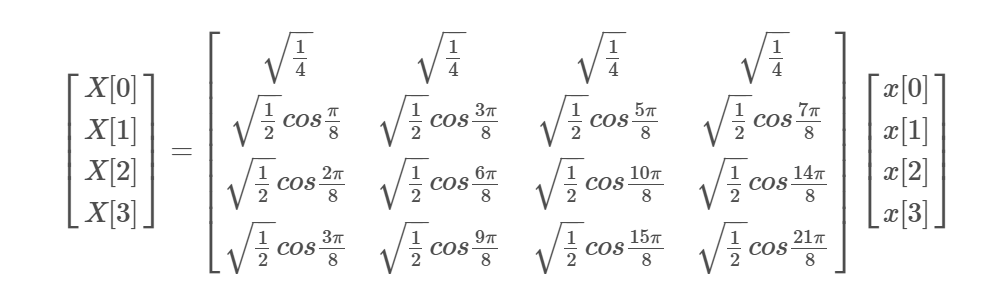
我们暂且将中间的矩阵称为A矩阵,则X[μ] = Ax[n]
这里的E(μ)是归一化系数,满足下图情况,它可以使得矩阵A保持正交。
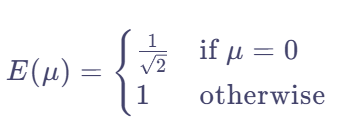
我们输入为几个,就可以相对应获得几个DCT系数。一维离散余弦变换的C语言实现如下
#include <stdio.h>
#include <stdint.h>
#include <stdio.h>
#include <math.h>
#define N 8 //输入信号的长度
void dct(int input[], double output[]) {
double alpha;
double sum;
int i, j;
for (i = 0; i < N; i++) {
if (i == 0) {
alpha = sqrt(1.0 / N);
}
else {
alpha = sqrt(2.0 / N);
}
sum = 0;
for (j = 0; j < N; j++) {
sum += input[j] * cos((2 * j + 1) * i * M_PI / (2 * N));
}
output[i] = alpha * sum;
}
}
int main()
{
int input[N] = { 1,2,3,4,5,6,7,8 }; //输入信号
double output[N]; //变换后的信号
int i;
dct(input, output);
printf("DCT结果:");
for (i = 0; i < N; i++) {
printf("%lf\n", output[i]);
}
printf("\n");
return 0;
}
Python的代码实现如下
import numpy as np
def dct1d(x):
N = len(x)
X = np.zeros(N)
for k in range(N):
sum_val = 0.0
for n in range(N):
sum_val += x[n] * np.cos((np.pi / N) * (n + 0.5) * k)
alpha = np.sqrt(1.0 / N) if k == 0 else np.sqrt(2.0 / N)
X[k] = alpha * sum_val
return X
def main():
# 示例数据
x = [] # 输入的原始数据
# 计算DCT
X = dct1d(x)
# 打印结果
print("DCT结果:")
print(X)
if __name__ == "__main__":
main()逆离散余弦变换
DCT是可逆的,意味着我们可以通过逆DCT(IDCT)从频域信号恢复原始信号,前提是没有对DCT系数进行过度的削减。
逆离散余弦变换(IDCT)是离散余弦变换(DCT)的逆过程,IDCT的全称是Inverse Discrete Cosine Transform。
直接贴一个解密Python脚本
import numpy as np
s1=[]
#待解密数据
N=
#待解密数据数组长度
A = np.array([[np.cos((j + 0.5) * i * np.pi / N) for j in range( N)] for i in range( N)])
b = np.array([s1[i] / np.sqrt(1.0 / N) if i == 0 else s1[i] / np.sqrt(2.0 / N) for i in range( N)])
solution, residuals, rank, s = np.linalg.lstsq(A, b, rcond=None)
print("Result:")
print(solution)这是C语言代码的是实现
#include <stdio.h>
#include <math.h>
#define N 8 // 变换长度
// 计算IDCT
void idct(float* input, float* output) {
int u, x;
float sum;
// IDCT的余弦系数
float Cx, Cu;
float pi = 3.14159265358979323846;
// IDCT公式计算
for (x = 0; x < N; ++x) {
sum = 0.0;
for (u = 0; u < N; ++u) {
if (u == 0) {
Cu = sqrt(1.0 / N);
}
else {
Cu = sqrt(2.0 / N);
}
Cx = cos((2 * x + 1) * u * pi / (2 * N));
sum += Cu * input[u] * Cx;
}
output[x] = sum;
}
}
int main() {
float input[N] = { }; // 输入的DCT系数
float output[N]; // 解密后的时域信号
// 计算IDCT
idct(input, output);
// 打印结果
printf("IDCT Result:\n");
for (int i = 0; i < N; i++) {
printf("%f ", output[i]);
}
printf("\n");
return 0;
}
建议还是用Python代码,即简便,而且可能没有C语言那么容易出现问题。