又来补加密算法了
SM4(原名SMS4.0)是中华人民共和国政府采用的一种分组密码标准,由国家密码管理局于2012年3月21日发布。相关标准为“GM/T 0002-2012《SM4分组密码算法》(原SMS4分组密码算法)”。
SM4是一种分组加密,是我们大中华的加密算法,所有也叫国密,它也是对称密码算法。
这里我们明确两个概念吧,一个是分组加密,一个是对称加密算法,写了那么多加密算法的文章,其实它们已经出现很多次了。分组密码就是将我们所要加密的明文一开始就切成一段段的,放入数组当中,然后分组加密,再拼接成密文,有时候密钥也会被分组。
而对称加密算法就是(也叫私钥加密)指加密和解密使用相同密钥的加密算法。有时又叫传统密码算法,就是加密密钥能够从解密密钥中推算出来,同时解密密钥也可以从加密密钥中推算出来。而在大多数的对称算法中,加密密钥和解密密钥是相同的,所以也称这种加密算法为秘密密钥算法或单密钥算法。它要求发送方和接收方在安全通信之前,商定一个密钥。对称算法的安全性依赖于密钥,泄漏密钥就意味着任何人都可以对他们发送或接收的消息解密,所以密钥的保密性对通信的安全性至关重要。
上面信息来自百度
SM4加密
SM4的明文长度是128bit,平均分为四组,密钥的长度也是128bit。
其加解密过程采用了32轮迭代机制(与DES、AES类似),每一轮需要一个轮密钥。
所以SM4加密分为两个模块,一部分是加密模块,另一部分是密钥扩展模块。这些模块中包含的运算操作主要有:异或运算、移位变换、盒变换。
盒变换说的就是S盒,AES也有对吧,这个S盒的全称其实就是Substitution Box,Substitution的含义是替换,替代,也就是替换盒,S盒在加密算法当中的作用几乎都是差不多的。
说说这里SM4怎么通过输入S盒的数据进行替换,一般输入S盒的数据长度为8bit,然后就转换成16进制的数据。比如11001010转换成16进制后就是CA,然后到S盒里面找第C行第A列,替换之后就是5C。
SM4的S盒如下
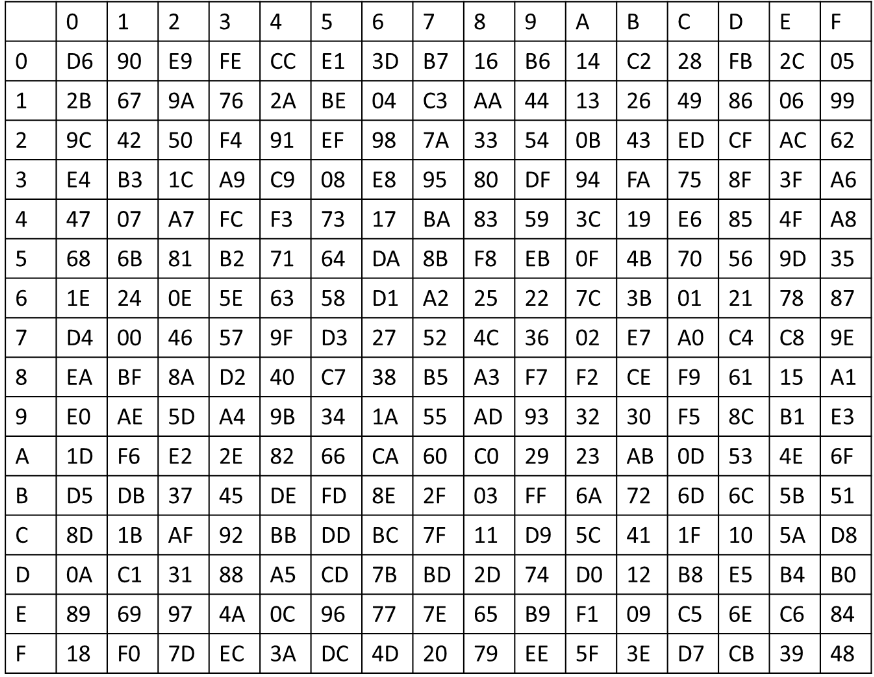
密钥扩展模块
我们得先介绍密钥扩展模块
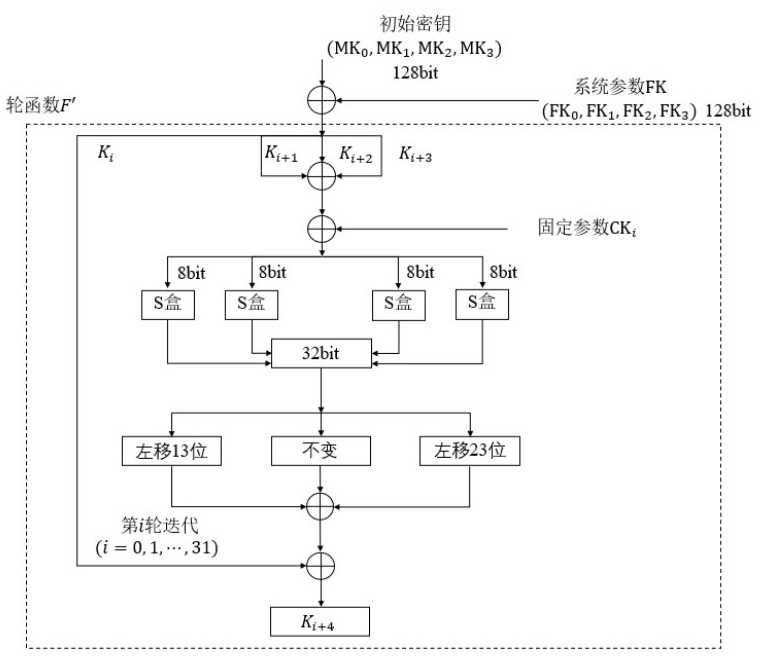
输入的原始密钥 key 为 128bit 的数据,将其按位拆分成 4 个 32bit 的数据 K0,K1,K2,K3,
将初始密钥 K0, K1, K2, K3分别异或固定参数 FK0, FK1, FK2, FK3 得到用于循环的密钥 k0, k1, k2, k3。
即 k0=K0⊕FK0, k1=K1⊕FK1, k2=K2⊕FK2,k3=K3⊕FK3, k0=K0⊕FK0, k1=K1⊕FK1, k2=K2⊕FK2, k3=K3⊕FK3,这里的⊕是异或的数学符号,额(⊙﹏⊙),我也是第一次知道,因为只用^。
这里的固定参数在官方文档里面。
官方文档链接:gmbz.org.cn/main/viewfile/20180108015408199368.html
文档里面那个奇奇怪怪的符号应该是A
进入轮函数当中,i=0 时为第一次轮变换,一直进行到i=31结束。然后上图中的Ki暂时不做处理,然后令另外三个Ki+1、Ki+2、Ki+3和固定参数 CKi异或得到一个 32bit 的数据,作为盒变换的输入。一开始这个Ki,和另外三个Ki+1、Ki+2、Ki+3的大概意思,举个例子,比如第一轮函数,Ki就是K0,函数结束会得到一个K4,然后第二轮加密Ki就变成了K1,而Ki+3就是上一轮新生成的K4,以此类推。
所以sbox_input=Ki^Ki+1^Ki+2^CKi,将这个盒输入拆成4个8bit长度的数据,然后我们再得到4个盒输出,合并起来就是盒输出sbox_output,然后左移13位,得到一个数据y13,右移23位,得到另外一个数据y23。
然后再将盒输出和y13、y23、ki,进行异或即可得到轮密钥,也是下一轮函数的Ki+3
也就是rki=Ki+4=y13^y23^Ki^sbox_output。总共产生32个轮密钥,用于32轮加密函数当中。这篇博客讲的很详细
SM4加密算法原理和简单实现(java) – kentle – 博客园 (cnblogs.com)
里面的java代码也很好理解,以下就是密钥扩展模块的Java代码实现。
int[] key_r;
/* 初始化轮密钥 */
SM4(byte[] key) {
this.key_r = keyGenerate(key);
}
/* 密钥拓展 */
private int[] keyGenerate(byte[] key) {
int[] key_r = new int[32];//轮密钥rk_i
int[] key_temp = new int[4];
int box_in, box_out;//盒变换输入输出
final int[] FK = {0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc};
final int[] CK = {
0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279
};
//将输入的密钥每32比特合并,并异或FK
for (int i = 0; i < 4; i++) {
key_temp[i] = jointBytes(key[4 * i], key[4 * i + 1], key[4 * i + 2], key[4 * i + 3]);
key_temp[i] = key_temp[i] ^ FK[i];
}
//32轮密钥拓展
for (int i = 0; i < 32; i++) {
box_in = key_temp[1] ^ key_temp[2] ^ key_temp[3] ^ CK[i];
box_out = sBox(box_in);
key_r[i] = key_temp[0] ^ box_out ^ shift(box_out, 13) ^ shift(box_out, 23);
key_temp[0] = key_temp[1];
key_temp[1] = key_temp[2];
key_temp[2] = key_temp[3];
key_temp[3] = key_r[i];
}
return key_r;
}加密模块
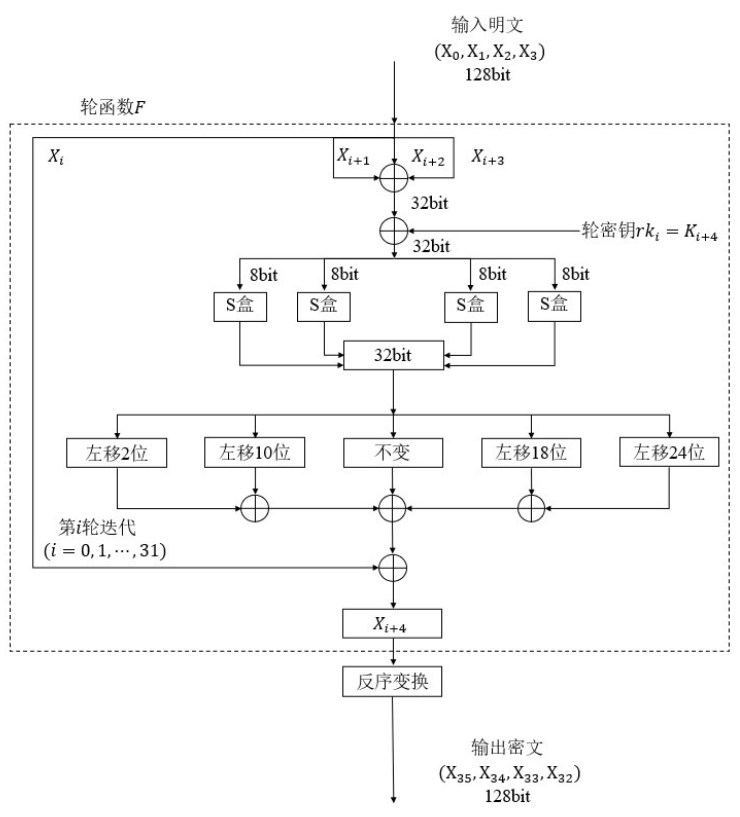
这是加密的流程图,首先将明文分为四组,每组长度为32bit,然后轮函数和密钥扩展模块的轮函数差不多,Xi先不处理,这里的盒输入sbox_input=Xi+1^Xi+2^Xi+3^rki(这里我直接用计算机的异或符号了),然后再通过一个盒变换得到一个盒输出,再位移对吧,和密钥扩展一样,只不过这里数据比较多,最后都将它们异或。
最后的Xi+4=y2^y10^y18^y24^sbox_output^Xi,然后这个Xi+4会继续在下一轮加密当中发挥作用,
将轮函数F最后生成的4个32bit数据X32、X33、X34、X35,合并后执行反序变换操作,得到最终的128bit的密文数据,反序就是反转顺序,最后的密文就是X35、X34、X33、X32。
其实加密流程还是挺清晰的。以下是SM4加密的C++实现
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
string BinToHex(string str) {//二进制转换为十六进制的函数实现
string hex = "";
int temp = 0;
while (str.size() % 4 != 0) {
str = "0" + str;
}
for (int i = 0; i < str.size(); i += 4) {
temp = (str[i] - '0') * 8 + (str[i + 1] - '0') * 4 + (str[i + 2] - '0') * 2 + (str[i + 3] - '0') * 1;
if (temp < 10) {
hex += to_string(temp);
}
else {
hex += 'A' + (temp - 10);
}
}
return hex;
}
string HexToBin(string str) {//十六进制转换为二进制的函数实现
string bin = "";
string table[16] = { "0000","0001","0010","0011","0100","0101","0110","0111","1000","1001","1010","1011","1100","1101","1110","1111" };
for (int i = 0; i < str.size(); i++) {
if (str[i] >= 'A' && str[i] <= 'F') {
bin += table[str[i] - 'A' + 10];
}
else {
bin += table[str[i] - '0'];
}
}
return bin;
}
int HexToDec(char str) {//十六进制转换为十进制的函数实现
int dec = 0;
if (str >= 'A' && str <= 'F') {
dec += (str - 'A' + 10);
}
else {
dec += (str - '0');
}
return dec;
}
string LeftShift(string str, int len) {//循环左移len位函数实现
string res = HexToBin(str);
res = res.substr(len) + res.substr(0, len);
return BinToHex(res);
}
string XOR(string str1, string str2) {//异或函数实现
string res1 = HexToBin(str1);
string res2 = HexToBin(str2);
string res = "";
for (int i = 0; i < res1.size(); i++) {
if (res1[i] == res2[i]) {
res += "0";
}
else {
res += "1";
}
}
return BinToHex(res);
}
string NLTransform(string str) {//非线性变换t函数实现
string Sbox[16][16] = { {"D6","90","E9","FE","CC","E1","3D","B7","16","B6","14","C2","28","FB","2C","05"},
{"2B","67","9A","76","2A","BE","04","C3","AA","44","13","26","49","86","06","99"},
{"9C","42","50","F4","91","EF","98","7A","33","54","0B","43","ED","CF","AC","62"},
{"E4","B3","1C","A9","C9","08","E8","95","80","DF","94","FA","75","8F","3F","A6"},
{"47","07","A7","FC","F3","73","17","BA","83","59","3C","19","E6","85","4F","A8"},
{"68","6B","81","B2","71","64","DA","8B","F8","EB","0F","4B","70","56","9D","35"},
{"1E","24","0E","5E","63","58","D1","A2","25","22","7C","3B","01","21","78","87"},
{"D4","00","46","57","9F","D3","27","52","4C","36","02","E7","A0","C4","C8","9E"},
{"EA","BF","8A","D2","40","C7","38","B5","A3","F7","F2","CE","F9","61","15","A1"},
{"E0","AE","5D","A4","9B","34","1A","55","AD","93","32","30","F5","8C","B1","E3"},
{"1D","F6","E2","2E","82","66","CA","60","C0","29","23","AB","0D","53","4E","6F"},
{"D5","DB","37","45","DE","FD","8E","2F","03","FF","6A","72","6D","6C","5B","51"},
{"8D","1B","AF","92","BB","DD","BC","7F","11","D9","5C","41","1F","10","5A","D8"},
{"0A","C1","31","88","A5","CD","7B","BD","2D","74","D0","12","B8","E5","B4","B0"},
{"89","69","97","4A","0C","96","77","7E","65","B9","F1","09","C5","6E","C6","84"},
{"18","F0","7D","EC","3A","DC","4D","20","79","EE","5F","3E","D7","CB","39","48"} };
string res = "";
for (int i = 0; i < 4; i++) {
res = res + Sbox[HexToDec(str[2 * i])][HexToDec(str[2 * i + 1])];
}
return res;
}
string LTransform(string str) {//线性变换L函数实现
return XOR(XOR(XOR(XOR(str, LeftShift(str, 2)), LeftShift(str, 10)), LeftShift(str, 18)), LeftShift(str, 24));
}
string L2Transform(string str) {//线性变换L'函数实现
return XOR(XOR(str, LeftShift(str, 13)), LeftShift(str, 23));
}
string T(string str) {//用于加解密算法中的合成置换T函数实现
return LTransform(NLTransform(str));
}
string T2(string str) {//用于密钥扩展算法中的合成置换T函数实现
return L2Transform(NLTransform(str));
}
string KeyExtension(string MK) {//密钥扩展函数实现
string FK[4] = { "A3B1BAC6", "56AA3350", "677D9197", "B27022DC" };
string CK[32] = { "00070E15", "1C232A31", "383F464D", "545B6269",
"70777E85", "8C939AA1", "A8AFB6BD", "C4CBD2D9",
"E0E7EEF5", "FC030A11", "181F262D", "343B4249",
"50575E65", "6C737A81", "888F969D", "A4ABB2B9",
"C0C7CED5", "DCE3EAF1", "F8FF060D", "141B2229",
"30373E45", "4C535A61", "686F767D", "848B9299",
"A0A7AEB5", "BCC3CAD1", "D8DFE6ED", "F4FB0209",
"10171E25", "2C333A41", "484F565D", "646B7279" };
string K[36] = { XOR(MK.substr(0,8),FK[0]),XOR(MK.substr(8,8),FK[1]),XOR(MK.substr(16,8),FK[2]),XOR(MK.substr(24),FK[3]) };
string rks = "";
for (int i = 0; i < 32; i++) {
K[i + 4] = XOR(K[i], T2(XOR(XOR(XOR(K[i + 1], K[i + 2]), K[i + 3]), CK[i])));
rks += K[i + 4];
}
return rks;
}
string encode(string plain, string key) {//加密函数实现
cout << "轮密钥与每轮输出状态:" << endl;
cout << endl;
string cipher[36] = { plain.substr(0,8),plain.substr(8,8),plain.substr(16,8),plain.substr(24) };
string rks = KeyExtension(key);
for (int i = 0; i < 32; i++) {
cipher[i + 4] = XOR(cipher[i], T(XOR(XOR(XOR(cipher[i + 1], cipher[i + 2]), cipher[i + 3]), rks.substr(8 * i, 8))));
cout << "rk[" + to_string(i) + "] = " + rks.substr(8 * i, 8) + " X[" + to_string(i) + "] = " + cipher[i + 4] << endl;
}
cout << endl;
return cipher[35] + cipher[34] + cipher[33] + cipher[32];
}
string decode(string cipher, string key) {//解密函数实现
cout << "轮密钥与每轮输出状态:" << endl;
cout << endl;
string plain[36] = { cipher.substr(0,8),cipher.substr(8,8), cipher.substr(16,8), cipher.substr(24,8) };
string rks = KeyExtension(key);
for (int i = 0; i < 32; i++) {
plain[i + 4] = XOR(plain[i], T(XOR(XOR(XOR(plain[i + 1], plain[i + 2]), plain[i + 3]), rks.substr(8 * (31 - i), 8))));
cout << "rk[" + to_string(i) + "] = " + rks.substr(8 * (31 - i), 8) + " X[" + to_string(i) + "] = " + plain[i + 4] << endl;
}
cout << endl;
return plain[35] + plain[34] + plain[33] + plain[32];
}
int main() {//主函数
string str = "0123456789ABCDEFFEDCBA9876543210";
cout << "明 文:" << str.substr(0, 8) << " " << str.substr(8, 8) << " " << str.substr(16, 8) << " " << str.substr(24, 8) << endl;
cout << endl;
string key = "0123456789ABCDEFFEDCBA9876543210";
cout << "加密密钥:" << key.substr(0, 8) << " " << key.substr(8, 8) << " " << key.substr(16, 8) << " " << key.substr(24, 8) << endl;
cout << endl;
string cipher = encode(str, key);
cout << "密 文:" << cipher.substr(0, 8) << " " << cipher.substr(8, 8) << " " << cipher.substr(16, 8) << " " << cipher.substr(24, 8) << endl;
cout << endl;
cout << "密 文:" << cipher.substr(0, 8) << " " << cipher.substr(8, 8) << " " << cipher.substr(16, 8) << " " << cipher.substr(24, 8) << endl;
cout << endl;
cout << "解密密钥:" << key.substr(0, 8) << " " << key.substr(8, 8) << " " << key.substr(16, 8) << " " << key.substr(24, 8) << endl;
cout << endl;
string plain = decode(cipher, key);
cout << "明 文:" << plain.substr(0, 8) << " " << plain.substr(8, 8) << " " << plain.substr(16, 8) << " " << plain.substr(24, 8) << endl;
}
以上代码输出密文是 681EDF34 D206965E 86B3E94F 536E4246 ,刚好128bit,但是我们会发现,我们在一些在线网站当中加密,会得到长度比256bit的密文,但是前128bit长度还是相同,如图
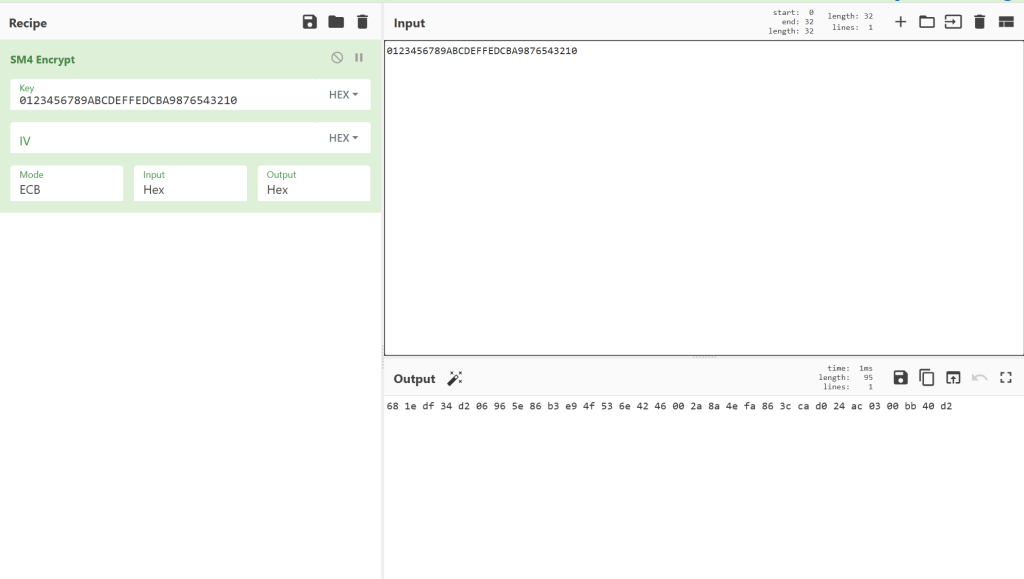
我在这里疑惑了好久,最后发现它是一种填充方式,在上面那个博文链接里面也有提及,默认应该是PKCS7的填充方式,我试了一下,在同一密钥的情况之下,无论明文是多少,后面填充的128bit都是相同的。
关于这个填充方式,以及填充的128bit是怎么得来的就不在这提及了,应该挺复杂的,以后有机会再详细学习。

