CTF的Reverse方向,在一开始做题的时候经常会遇到TEA加密,之前遇到就想着拖一拖再学习,最近学长给上课让我们做小测试,有些不会有点小尴尬。最近我是要抽时间把这些经常遇到的加密算法都补完了。 有关加密算法的详细过程我经常看B站up主Litt1eQ的视频,不过他做视频好像也没有继续坚持下去了。
该up主关于TEA加密算法的学习视频
【动画密码学】TEA(Tiny Encryption Algorithm)|分组加密_哔哩哔哩_bilibili
“TEA” 的全称为”Tiny Encryption Algorithm” ,是1994年由英国剑桥大学的David j.wheeler发明的。
TEA加密
首先先放上TEA加密算法的C语言实现,代码如下:
#include <stdio.h>
void encrypt (unsigned int* v, unsigned int* k) {
unsigned int v0=v[0], v1=v[1], sum=0, i;
unsigned int delta=0x9e3779b9;
unsigned int k0=k[0], k1=k[1], k2=k[2], k3=k[3];
for (i=0; i < 32; i++) {
sum += delta;
v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
}
v[0]=v0; v[1]=v1;
}首先在TEA加密过程中有两个常量我们要知道。
第一个就是上图代码中的32,这是TEA加密的轮数,32轮循环,总共32轮加密,这个次数是TEA的作者推荐的,当然也会有64轮,16轮啥的。
第二个常数就是上图代码中的delta,它的值为0x9e3779b9,关于它的来源如下图所示,来自书本《加密与解密》当中。

至于为啥是选择这个,我也不知道。但是有时候它并不会以这样的形式出现,一般情况下是sum +=0x9e3779b9
但有时候会以sum – = 0x61C88647的情况出现,这两种情况其实是等价的,-0x61C88647作为负数,它的补码等于0x9e3779b9,所以在C/C++中是等价的,可以用下面的代码验证
int v3=0;
v3 -= 0x61C88647;
if(v3==0x9e3779b9){
printf("equal\n");
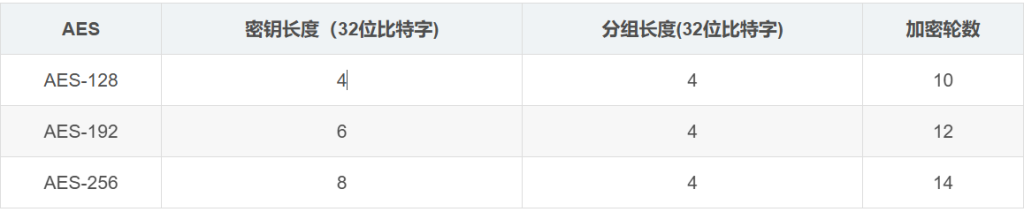
}然后TEA加密过程中也和其他加密算法一样,有两个最基本的元素,明文与密钥,明文分组长度为64位(8字节),密钥长度为128位(16字节),它这里我一开始也不知道为啥明文还有分组长度,其实就是明文在加密过程中是分组的,其总长度就是64.
我们学习加密中的详细过程,其实主要学习它第一轮加密干了啥就行了。首先先看它的初始化
#include <stdio.h>
void encrypt (unsigned int* v, unsigned int* k) {
unsigned int v0=v[0], v1=v[1], sum=0, i;
unsigned int delta=0x9e3779b9;
unsigned int k0=k[0], k1=k[1], k2=k[2], k3=k[3]; 这里我们传入的v就是明文,k就是密钥,看初始化我们会很奇怪为什么明文v的长度不是64位吗?为什么只对v[0]和v[1]即明文的前两位进行,其实实际上是将明文放入了一个数组当中,分为了两组,我们拿上面的视频来举例
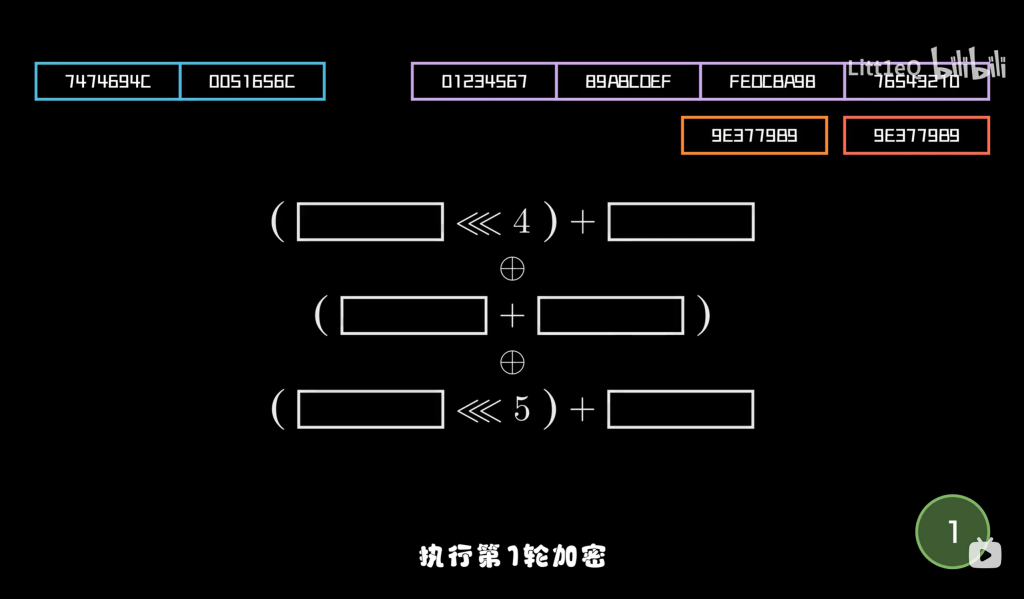
如图,假设左上角的蓝色框内7474694C 0051656C就是我们TEA加密的明文,它是小端序的存储方式,实际的明文应该是4C6974746C655100,我也不知道up主为啥要搞成小端序的存储方式,我们在文章里面就直接说框里数字得了。观察明文,是16进制,总共有16位,也就是刚刚好8个字节,长度64位符合TEA加密的明文长度,然后将其分为了两组,第一组是v0,为7474694C,第二组为v1,为0051656C。
然后右上角的紫色框内就是密钥,总共32个16进制位,长度也就是128位。然后将其分成了4组,k0,k1,k2,k3。
红色框内既是常数delta,橙色框内是第一轮加密前sum值初始化,等于delta的值。再来看加密部分
for (i=0; i < 32; i++) {
sum += delta;
v0 += ((v1<<4) + k0)^(v1 + sum)^((v1>>5) + k1);
v1 += ((v0<<4) + k2)^(v0 + sum)^((v0>>5) + k3);
}
v[0]=v0; v[1]=v1;
}每一轮加密前sum = sum + delta,一开始sum的值为0,所以第一轮开始前sum等于delta的值。然后就是对各种数异或操作,使得明文的值被改变。这里感觉没啥好说的,左移右移异或。
两个执行完加密操作后明文就变了,在这过程中密钥的值是不变的,而参与异或过程的sum,每一轮过后都会再加一次delta的值,sum = 轮数 × delta 。
好啦,加密过程讲完了,TEA的加密还算毕竟少的,实现非常简单,很精短。
TEA解密
TEA加密的过程当中运用了移位和异或,没有什么不可逆的运算,所有TEA加密算法是可逆的,也就是说,它是可以由密文解密再得到明文的。解密代码如下:
void decrypt (uint32_t *v,uint32_t *k){
uint32_t v0=v[0],v1=v[1],sum=0xC6EF3720,i;
//这里的sum是0x9e3779b9*32后截取32位的结果,截取很重要。
uint32_t delta=0x9e3779b9;
uint32_t k0=k[0],k1=k[1],k2=k[2],k3=k[3];
for (i=0;i<32;i++){
v1-=((v0<<4) + k2)^(v0 + sum)^((v0>>5) + k3);
v0-=((v1<<4) + k0)^(v1 + sum)^((v1>>5) + k1);
sum-=delta;
}
可以看到初始化的时候 sum = delta×32,后面每进行一轮解密,sum = sum – delta,这里还是很好理解的。
我们看加密的最后一步 v1 = v1 + ((v0<<4) + k2)^(v0 + sum)^((v0>>5) + k3); 等式右边的v1就是加密了一轮之后上一轮的v1,解密过程中就是还原这个值。
所以就有了解密第一步还原上一轮初始的v1,v1 = v1 – ((v0<<4)+k2)^(v0+sum)^((v0>>5)+k3);
这里可以解密还有一点是加密过程中是先加密v0,再加密v1的,所以可以用v0来先还原v1,还原了v1之后,就能再用这个v1来还原v0了。这个解密过程但看我说的文字可能还是有些难以理解的,还是需要自己去看代码来理解。
TEA加密算法的文章就这样说完了。